[LeetCode] 005. Longest Palindrome
-
date_range Mar. 26, 2019 - Tuesday info
- Problem (Medium)
- Approach 1: Longest Common Substring
- Approach 1 Update: Improve Space Complexity
- Approach 2: Brute Force
- Approach 3: Dynamic Programming (Improving the Brute Force)
- Solution 3 Update: Improve Space Complexity
- Approach 4: Expand Around Center
- Approach 5: Manacher’s Algorithm ($O(n)$)
Problem (Medium)
005. Longest Palindromic Substring
Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.
Example 1:
Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.
Example 2:
Input: "cbbd"
Output: "bb"
Approach 1: Longest Common Substring
Apply Dynamic Programming to find the longest common substring, check the index.
Idea
- Reverse the string $S$ to $S’$, find the longest common substring between $S$ and $S’$;
- Check the index of the found common substring in $S$ and $S’$ to fix counter cases like “abcdefcba” (whose reverse is “abcfedcba” -> common sub is “abc” which is wrong).
Dynamic Update Rule:
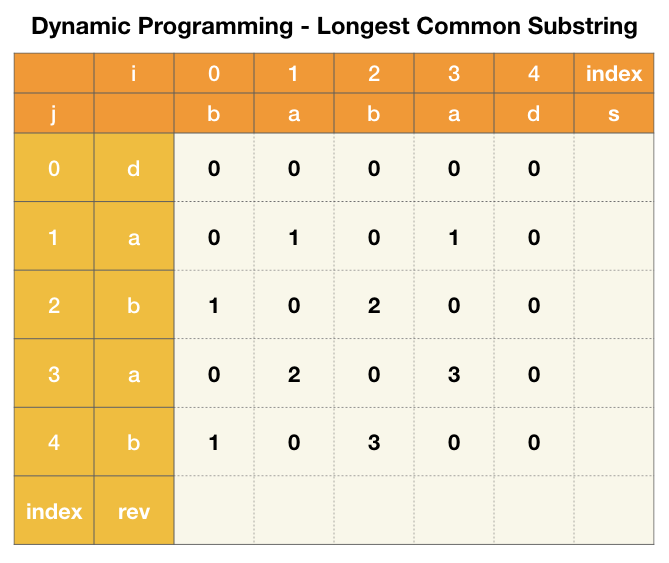
Check index of:
- i - dp[i][j] + 1 == len(s) - 1 - j
Solution
class Solution1:
def longestPalindrome(self, s: str) -> str:
if s is "":
return ""
rev = s[::-1]
dp = [[0 for i in range(len(s))] for j in range(len(s))]
max_len = 0
max_end = 0
for i in range(len(s)):
for j in range(len(s)):
if s[i] == rev[j]:
if i == 0 or j == 0:
dp[i][j] = 1
else:
dp[i][j] = dp[i-1][j-1] + 1
if dp[i][j] > max_len:
if i-dp[i][j]+1 == len(s)-1-j:
max_len = dp[i][j]
max_end = i
return s[max_end - max_len + 1: max_end + 1]
Complexity
- Time Complexity: $O(n^2)$
- Space Complexity: $O(n^2)$
Approach 1 Update: Improve Space Complexity
Idea
In the double loop above, we notice that we only need the previous column for the update of each column of $i$. Thus we can change the “dp” to 1-D array.
Solution
class Solution1_update:
def longestPalindrome(self, s: str) -> str:
if s is "":
return ""
rev = s[::-1]
dp = [0 for i in range(len(s))]
max_len = 0
max_end = 0
for i in range(len(s)):
# Updated the loop order
for j in range(len(s)-1, -1, -1):
if s[i] == rev[j]:
if i == 0 or j == 0:
dp[j] = 1
else:
dp[j] = dp[j-1] + 1
# Updated here - new columns should be updated on conditions
else:
dp[j] = 0
if dp[j] > max_len:
if i-dp[j]+1 == len(s)-1-j:
max_len = dp[j]
max_end = i
return s[max_end - max_len + 1: max_end + 1]
Approach 2: Brute Force
Idea
Just pick all possible substrings to verify if it’s a palindrome.
But it cannot be accepted by LC, because the “Time Limit Exceeded!”
Solution
class Solution2:
def longestPalindrome(self, s: str) -> str:
def isPalindrome(s):
if s is "":
return False
for i in range(len(s)//2):
if s[i] != s[-1-i]:
return False
return True
common_subs = {}
if s is "":
return ""
for i in range(len(s)):
for j in range(1, len(s)+1):
if isPalindrome(s[i:j]):
common_subs[s[i:j]] = len(s[i:j])
return max(common_subs, key=common_subs.get)
Complexity Analysis
- Time Complexity: $O(n^3)$
- Space Complexity: $O(1)$
Approach 3: Dynamic Programming (Improving the Brute Force)
Idea
We can save some repeated computation in the brute force.
First, we define a function $P$:
Thus,
The base cases are:
This yields a straight forward DP solution, which we first initialize the one and two letters palindromes, and work our way up finding all three letters palindromes, and so on…
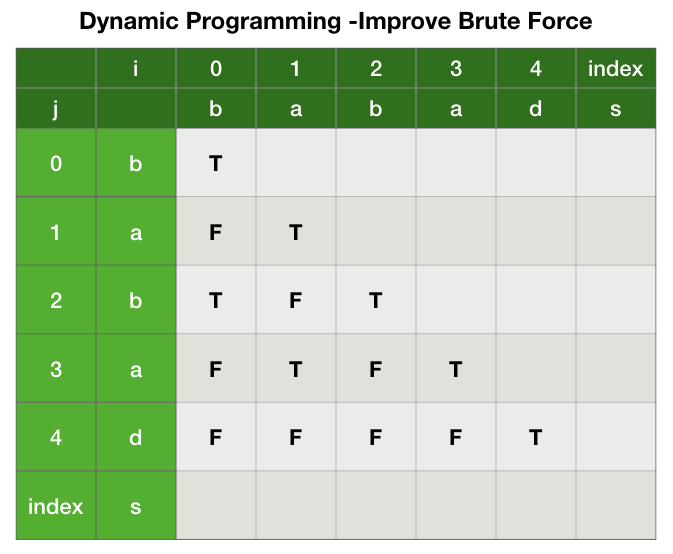
Solution
class Solution3:
def longestPalindrome(self, s: str) -> str:
if s is "":
return s
res = ""
dp = [[None for i in range(len(s))] for j in range(len(s))]
for j in range(len(s)):
for i in range(j+):
if i == j:
dp[j][i] = True
elif j == i+1:
dp[j][i] = (s[i] == s[j])
else:
dp[j][i] = (dp[j-1][i+1] and s[i] == s[j])
if dp[j][i] and j - i + 1 > len(res):
res = s[i:j+1]
return res
Complexity Analysis
- Time Complexity: $O(n^2)$
- Space Complexity: $O(n^2)$
Solution 3 Update: Improve Space Complexity
Idea
or each line of j, dp only depends on previous line of j. Thus, we just need a n by 1 array instead of n by n matrix.
Solution
class Solution3:
def longestPalindrome(self, s: str) -> str:
if s is "":
return s
res = ""
dp = [None for i in range(len(s))]
for j in range(len(s)):
for i in range(j+1):
if i == j:
dp[i] = True
elif j == i+1:
dp[i] = (s[i] == s[j])
else:
dp[i] = (dp[i+1] and s[i] == s[j])
if dp[i] and j - i + 1 > len(res):
res = s[i:j+1]
return res
Complexity Analysis
- Time Complexity: $O(n^2)$
- Space Complexity: $O(n)$
Approach 4: Expand Around Center
Idea
- a palindrome can be expanded from its center;
- there are $2n-1$ such centers (odd and even palindromes: $n + (n-1)$).
Solution
class Solution4:
def longestPalindrome(self, s: str) -> str:
if s is '':
return s
max_len = 0
start, end = 0, 0
for i in range(len(s)):
len1 = self.expandFromCenter(s, i, i)
len2 = self.expandFromCenter(s, i, i+1)
l = max(len1, len2)
if l > end - start:
start = i - (l - 1) // 2
end = i + l // 2
return s[start:end+1]
def expandFromCenter(self, s, idx1, idx2):
while idx1 >= 0 and idx2 < len(s) and s[idx1] == s[idx2]:
idx1 -= 1
idx2 += 1
return idx2 - idx1 - 1
Complexity Analysis
- Time Complexity: $O(n^2)$
- Space Complexity: $O(1)$
Approach 5: Manacher’s Algorithm ($O(n)$)
Idea
This is a non-trivial method which only have an $O(n)$ time complexity. Check out this link
Solution
Manacher’s algorithm solution in python:
class Solution5:
def longestPalindrome(self, s: str) -> str:
N = len(s)
if N < 2:
return s
N = 2*N+1 # Position count
L = [0] * N
L[0] = 0
L[1] = 1
C = 1 # centerPosition
R = 2 # centerRightPosition
i = 0 # currentRightPosition
iMirror = 0 # currentLeftPosition
maxLPSLength = 0
maxLPSCenterPosition = 0
start = -1
end = -1
diff = -1
for i in range(2, N):
# get currentLeftPosition iMirror for currentRightPosition i
iMirror = 2*C-i
L[i] = 0
diff = R - i
# If currentRightPosition i is within centerRightPosition R
if diff > 0:
L[i] = min(L[iMirror], diff)
# Attempt to expand palindrome centered at currentRightPosition i
# Here for odd positions, we compare characters and
# if match then increment LPS Length by ONE
# If even position, we just increment LPS by ONE without
# any character comparison
try:
while ((i + L[i]) < N and (i - L[i]) > 0) and \
(((i + L[i] + 1) % 2 == 0) or \
(s[(i + L[i] + 1) // 2] == s[(i - L[i] - 1) // 2])):
L[i]+=1
except Exception as e:
pass
if L[i] > maxLPSLength: # Track maxLPSLength
maxLPSLength = L[i]
maxLPSCenterPosition = i
# If palindrome centered at currentRightPosition i
# expand beyond centerRightPosition R,
# adjust centerPosition C based on expanded palindrome.
if i + L[i] > R:
C = i
R = i + L[i]
start = (maxLPSCenterPosition - maxLPSLength) // 2
end = start + maxLPSLength - 1
return s[start:end+1]
KF
